Graf

Graf merupakan pasangan tak berurutan yang terdiri dari himpunan tak kosong berupa titik/simpul (vertex) dan himpunan kosong berupa himpunan sisi (edge).

Jenis-jenis graf  

• Berdasarkan  ada tidaknya gelang atau sisi ganda pada suatu graf

   1. Graf sederhana

Graf yang tidak mengandung gelang maupun sisi ganda.

 

   2. Graf tak sederhana

Graf yang mengandung isi ganda atau gelang.

• Berdasarkan jumlah simpul pada suatu graf

   1. Graf berhingga

Graf berhingga adalah graf yang jumlah simpulnya n, berhingga.

   2. Graf tak berhingga

Graf yang tak berhingga ialah graf yang banyak simpulnya n, tak berhingga.

• Berdasarkan orientasi arah pada sisi

   1. Graf berarah

Graf yang setiap sisinya diberikan orientasi arah.

   2. Graf yang tak berarah

Graf yang sisinya tidak mempunyai orientasi arah

===================Terminologi Graf=====================

1. Bertetangga

   Dua buah simpul dikatakan bertetangga apabila keduanya terhubung langsung.

pada graf diatas : simpul P bertetangga sengan simpul Q dan S,tetapi
                            simpul P tidak bertetangga dengan simpul R

2. Bersisian

   Suatu sisi e dikatakan bersisian dengan simpul v1 dan sipul v2 jika e menghubungkan kesua simpul tersebut, dengan kata lain e=(v1,v2).

maka e1 berisian dengan simpul A dan sipul C, tetapi sisi tersebut tidak bersisian dengan simpul B.

3. Simpul terpencil

Simpul yang tidak mempunyai sisi yang bersisian dengannya.

simpul T dan simpul U merupakan simpul terpencil

4. Graf kosong

Graf yang himpunan sisinya merupakan himpunan kosong

5. Derajat

Derajat suatu simpul adalah jumlah sisi yang bersisian dengan simpul tersebut. Simpul yang berderajat 1 disebut anting-anting

6. Lintasan

Lintasan yang panjangnya n dari simpul awal v0 ke simpul tujuan vn didalam graf G ialah barisan yang berselang-selang simpul-simpul dan sisi-sisi yang berbentuk.

• pada graf tersebut lintasan P,Q,R memmiliki panjang 2, sementara lintasan P,Q,S,R memiliki panjang 3
• lintasan P,Q,R,S,P diamakan siklus atau sirkuit dengan panjang 4.
• antara simpul P dan U maupun T tidak dapat ditemukan lintasan.

7. Siklus atau sirkuit

Lintasan yang berawal dan berakhir pada simpul yang sana disebut sirkuit atau siklus.

Panjang sirkuit adalah jumlah sisi dalam sirkuit tersebut.

8. Terhubung

Dua buah simpul v1 dan simpul v2 disebut terhubung jika terdapat lintasan dari v1 ke v2.

9. Upagraf dan komplemen upagraf

Misalkan G = (V, E) adalah sebuah graf. G1 = (V1, E1) adalah upagraf dari G jika V1⊆ V dan
E1⊆ E.

Komplemen dari upagraf G1 terhadap G adalah graf G2 = (V2, E2) sedemikian sehingga E2 = E-E1 dan V2 adalah himpunan simpul yang anggota-anggota E2 bersisian sengannya.

Kompenen graf adalah jumlah maksimum upagraf terhubung dalam graf G.

10. Upagraf merentang

Upagraf G1 = (V1,E1) dari G= (V,E) dikatakan upagraf rentang jika V1=V (yaitu G1 mengandung semua simpul dari G).

11. Cut-Set

Cut-set dari graf terhubung G adalah himounan sisi yang bila dibuang dari G menyebabkan G tidak terhubung. Jadi, cut-set selalu menghasilkan dua buah kompenen .

pada graf tersebut, (1,4), (1,5), (2,3), (2,4) adalah cut-set. Terdapat banyak cut-set pada sebuag graf terhubung. Himpunan {(1,5), (4,5)} juga adalah cut-set, {(1,4), (1,5), (1,2)} adalah cut-set, {(5,6)} juga cut-set. tetapi {(1,4), (1,5), (4,5)} bukan cut-set sebab himpunan bagiannya {(1,5), (4,5)} adalah cut-set.

12. Graf berbobot

Graf berbobot adalah graf yang setiap sisinya diberi sebuah harga (bobot).

====================Graf Sederhana Khusus====================

   a. Graf lengkap

Graf lengkao ialah graf yang setiap simpulnya mempunyai sisi ke semua simpul lainnya.

   b. Graf lingkaran

Graf sederhana yang setiap simpulnya berderajat 2. Graf lingkaran dengan n simpul dilambangkan dengan Cn.

   c. Graf teratur

Graf teratur ialah graf yang setiap simpulnya mempunyai derajat yang sama.

   d. Graf bipatrit

Graf yang simpulnya dapat dikelompokkan menjadi dua himpunan bagian V1 dan V2, sedemikian sehingga setiap sisi di dalam G menghubungkan sebuah simpul di V1 ke sebuah simpul di V2 disebut graf bipatrit.

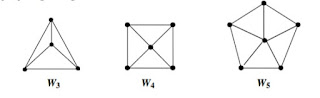
   e. Graf roda
Graf roda merupakan graf yang diperoleh dengan cara menambahkan satu simpul pada graf lingkaran Cn dan menghubungkan simpul baru tersebut  dengan sebuah simpul pada graf lingkaran tersebut.